Cuatro algoritmos de ordenación para ordenar una lista de elementos

Siguiendo con nuestro de programación en esta ocasión vamos a ver los algoritmos más conocidos para ordenar una lista de elementos. Estos algoritmos los podemos clasificar en dos grandes grupos según su complejidad:
- Algoritmos de complejidad cuadrática: Ordenamiento de burbuja (Bubblesort), ordenamiento por selección (Selection Sort) y ordenamiento por inserción (Insertion sort) entre otros, hay muchos más.
- Algoritmos de complejidad cuasi lineal o O(nlog(n)): solo veremos el rrdenamiento rápido o Quicksort pues para mi es el más sencillo de implementar y uno de los más eficaces aunque presente un cierto grado de inestabilidad.
Algoritmos de ordenación
Debemos tener claro lo que deben hacer estos algoritmos y básicamente es que a partir de una lista de elementos nuestros algoritmos la deben ordenar correctamente. Una práctica habitual, y como se debe empezar a desarrollar, es desarrollar siempre las pruebas más triviales antes de ponerse a desarrollar el algoritmo. También es recomendable definir las cabeceras de los métodos, para que no de errores de compilación la prueba.
Vamos a definir las cabeceras de nuestra clase. Nos centraremos únicamente en los métodos públicos, pues en la JUnits únicamente debemos interesarnos por el comportamiento de los métodos a los que podrá acceder el cliente.
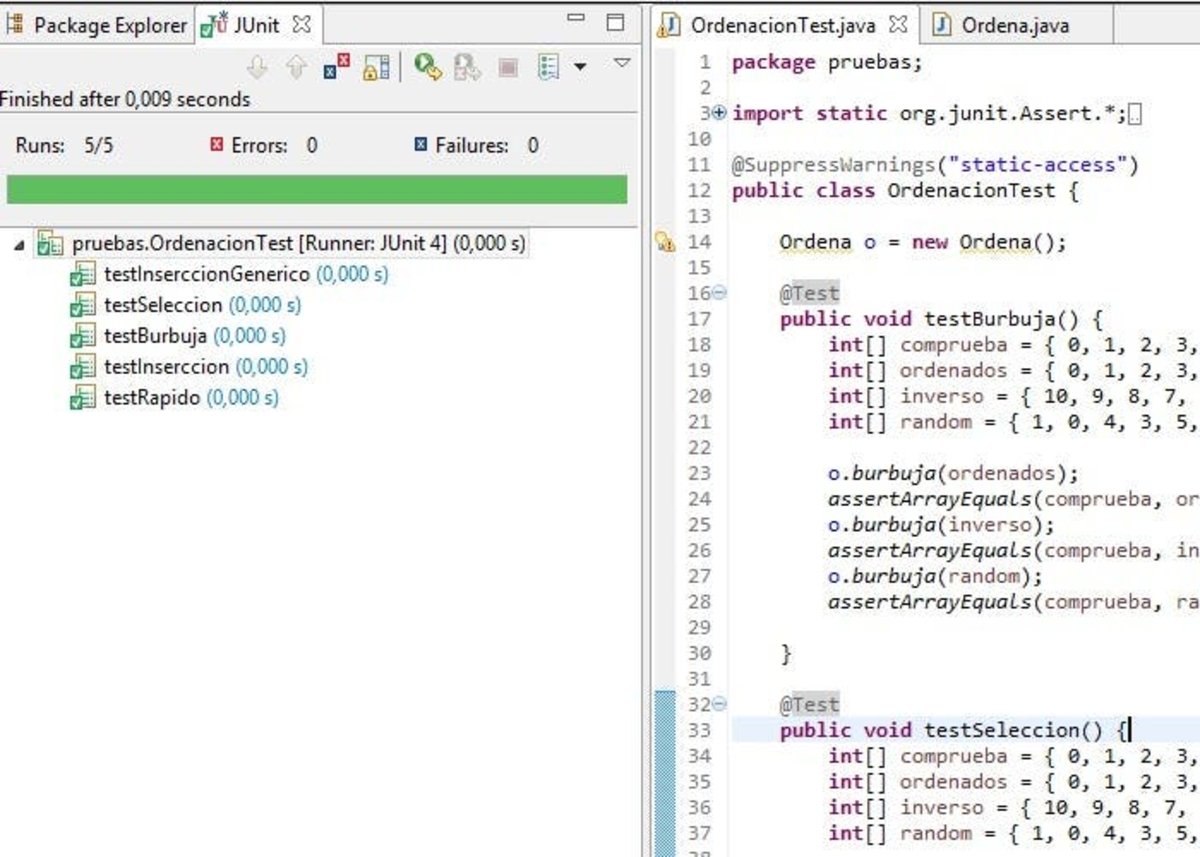
package source;public class Ordena {/** * Ordenación por el método de Burbuja * * @param a * array de enteros, después de la llamada quedará ordenado */public static void burbuja(int[] a) {}/** * Ordenación por inserción directa * * @param a * array de enteros, después de la llamada quedará ordenado */public static void insercion(int[] a) {}/** * Ordenación por el método rápido (quicksort) */public static void rapido(int[] v) {}/** * Ordenación por selección * * @param v * array de enteros, después de la llamada quedará ordenado */public static void seleccion(int[] v) {}}Vamos a definir la siguiente prueba unitaria:
package pruebas;import static org.junit.Assert.*;import org.junit.Test;import source.Ordena;@SuppressWarnings("static-access")public class OrdenacionTest {Ordena o = new Ordena();@Testpublic void testBurbuja() { int[] comprueba = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] ordenados = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] inverso = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }; int[] random = { 1, 0, 4, 3, 5, 10, 8, 9, 2, 6, 7 }; o.burbuja(ordenados); assertArrayEquals(comprueba, ordenados); o.burbuja(inverso); assertArrayEquals(comprueba, inverso); o.burbuja(random); assertArrayEquals(comprueba, random);}@Testpublic void testSeleccion() { int[] comprueba = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] ordenados = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] inverso = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }; int[] random = { 1, 0, 4, 3, 5, 10, 8, 9, 2, 6, 7 }; o.seleccion(ordenados); assertArrayEquals(comprueba, ordenados); o.seleccion(inverso); assertArrayEquals(comprueba, inverso); o.seleccion(random); assertArrayEquals(comprueba, random);}@Testpublic void testRapido() { int[] comprueba = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] ordenados = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] inverso = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }; int[] random = { 1, 0, 4, 3, 5, 10, 8, 9, 2, 6, 7 }; o.rapido(ordenados); assertArrayEquals(comprueba, ordenados); o.rapido(inverso); assertArrayEquals(comprueba, inverso); o.rapido(random); assertArrayEquals(comprueba, random);}@Testpublic void testInserccion() { int[] comprueba = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] ordenados = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; int[] inverso = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }; int[] random = { 1, 0, 4, 3, 5, 10, 8, 9, 2, 6, 7 }; o.insercion(ordenados); assertArrayEquals(comprueba, ordenados); o.insercion(inverso); assertArrayEquals(comprueba, inverso); o.insercion(random); assertArrayEquals(comprueba, random);}}Con la pruebas listas ya estamos preparados para programar nuestros algoritmos de ordenación. Algunos de los métodos utilizan una serie de algoritmos auxiliares:
private static void permuta(int[] a, int i, int j) { int t; t = a[i]; a[i] = a[j]; a[j] = t;}Lo que hace es cambiar dos elementos de sitio
private static int particion(int[] v, int iz, int de) { int i, pivote; permuta(v, (iz + de) / 2, iz); // el pivote es el de centro y se cambia con el primero pivote = v[iz]; i = iz; for (int s = iz + 1; s <= de; s++) if (v[s] <= pivote) { i++; permuta(v, i, s); } permuta(v, iz, i);// se restituye el pivote donde debe estar return i; // retorna la posicion en que queda el pivote}Método que va subdividiendo la lista en listas más pequeñas. Es un procedimiento recursivo denominado divide y vencerás.
Burbuja
El funcionamiento del algoritmo lo podéis ver desde su entrada de la wikipedia
Código:
public static void burbuja(int[] a) { int n = a.length; for (int i = 0; i <= n - 2; i++) for (int j = n - 1; j > i; j--) if (a[j - 1] > a[j]) permuta(a, j - 1, j);}Inserción
El funcionamiento del algoritmo lo podéis ver desde su entrada de la wikipedia
Código:
public static void insercion(int[] a) { int n = a.length; for (int i = 1; i <= n - 1; i++) { int x = a[i]; int j = i - 1; while (j >= 0 && x < a[j]) { a[j + 1] = a[j]; j = j - 1; } a[j + 1] = x; }}Selección
El funcionamiento del algoritmo lo podéis ver desde su entrada de la wikipedia
Código:
public static void seleccion(int[] v) { int n = v.length; int posmin; for (int i = 0; i < n - 1; i++) { posmin = i; for (int j = i + 1; j < n; j++) if (v[j] < v[posmin]) posmin = j;// posicion del mas pequeño permuta(v, i, posmin); } // for}Quicksort
El funcionamiento del algoritmo lo podéis ver desde su entrada de la wikipedia
Código:
private static void rapirec(int[] v, int iz, int de) { int m; if (de > iz) { m = particion(v, iz, de); rapirec(v, iz, m - 1); rapirec(v, m + 1, de); }}public static void rapido(int[] v) { rapirec(v, 0, v.length - 1);}Que algoritmo es mejor
Como siempre para comprobar esto tenemos que medir tiempos. Para ello haremos usado de tres métodos auxiliares para generar listas de tamaños grandes. Ponemos los siguientes métodos en nuestra clase pruebas:
/** * Este método da valores ordenados */private void ordenDirecto(int[] a) { int n = a.length; for (int i = 0; i < n; i++) a[i] = i;}/** * Este método da valores ordenados */private void ordenInverso(int[] a) { int n = a.length; for (int i = 0; i < n; i++) a[i] = n - i - 1;}/** * Este método da valores aleatorios a un vector de enteros, utiliza para * ello la clase Random del paquete java.util */private void aleatorio(int[] a) { Random r = new Random(); int n = a.length; for (int i = 0; i < n; i++) a[i] = r.nextInt(1000000);// valores entre 0 y 999999}Y para medir los tiempos podemos usar un método similar a este:
@Testpublic void testTiempos() { for (int n = 10000; n < 1000000000; n *= 2) { int[] v = new int[n]; ordenDirecto(v); // forma de generar la lista double t1 = System.currentTimeMillis(); o.seleccion(v); // ordenación double t2 = System.currentTimeMillis(); System.out.println("n=" + n + "**TIEMPO=" + (t2 - t1)); }}Vamos cambiando la forma de generar cada lista y el método de ordenación. Cuando lo hagamos con todas las combinaciones posibles tendremos un Excel similar a este. Debemos fijarnos que los algoritmos que hemos hecho solo funcionan para listas de enteros, podemos hacer que los algoritmos funcionen para cualquier tipo de objeto Comparable debemos hacer que nuestro método tenga por parámetro un tipo T comparable.
public void insercionComparable(T[] a) { int n = a.length; for (int i = 1; i <= n - 1; i++) { T x = a[i]; int j = i - 1; while (j >= 0 && x.compareTo(a[j]) < 0) { a[j + 1] = a[j]; j = j - 1; } a[j + 1] = x; }}Y además tenemos que acotar la genericidad de nuestra clase añadiendo el siguiente código a la cabecera de nuestra clase Ordena:
public class Ordena <T extends Comparable<T>> Podemos probar que funciona con por ejemplo objetos de tipo Persona con la siguiente prueba:
@Testpublic void testInserccionGenerico() { Persona[] comprueba = { new Persona(0), new Persona(1), new Persona(2), new Persona(3), new Persona(4), new Persona(5), new Persona(6) }; Persona [] random = { new Persona(5), new Persona(3), new Persona(2), new Persona(1), new Persona(4), new Persona(0), new Persona(6) }; o.insercionComparable(random); assertArrayEquals(comprueba, random); }Hasta aquí el artículo de hoy. Como siempre aquí tenéis el código fuente empleado.