Qué son las funciones recursivas

En este artículo vamos a tratar un tema que no es solo parte de nuestro curso de programación si no que es un recurso muy usado. Estamos hablando de las funciones recursivas, funciones que tienen la facultad de resolver un problema simplemente llamándose a si mismas.

Recursividad

La recursividad es la capacidad de una función para que se llame a sí mima, bien sea directa o indirectamente. Tenemos dos métodos de realizar un procedimiento (método o función) recursivo:

• Directa: función que se llama a si misma.
• Indirecta: función que llama a otra función y este última llama la primera.

Una definición recursiva debe constar de:

• Una o varias condiciones de parada.
• Una o varias condiciones por la que seguimos llamando a la función hasta dar con la solución (que se cumpla la condición de parada).

Ejemplo de calcular potencia de 2

Vamos a ver cinco formas de calcular la potencia de dos:

Primera forma: mediante una función iterativa, mediante un bucle sumando 2 en cada iteración.

public double pow2Iter(int n) {    double valor = 2;    if (n == 0)        return 1;    else        for (int i = 1; i < n; i++) {            valor += valor;        }    return valor;}

Segunda forma: mediante una función recursiva

public double pow2Rec(int n) {    if (n == 0)        return 1;    else        return 2 * pow2Rec(--n);}

Básicamente lo que hacemos es visitar cada nivel de un árbol de estado y calcular el valor de ese nivel en cada llamada y multiplicarlo por 2.

Tercera forma: mediante una función recursiva

public double pow2Rec2(int n) {    if (n == 0)        return 1;    else if (n == 1) {        return 2;    } else {        return pow2Rec2(--n) + pow2Rec2(n);    }}

Básicamente lo que hacemos es visitar cada elemento del nivel de un árbol de estado y calcular el valor de ese nivel en cada llamada y lo vamos sumando.Esta función será mucho más ineficiente que todas las demás, ya que las llamadas que se hacen de la función consiguen obtener una complejidad exponencial.

Cuarta forma: mediante una función recursiva

public double pow2Rec3(int n) {    if (n == 0)        return 1;    else if (n % 2 == 0)        return pow2Rec3(n / 2) * pow2Rec3(n / 2);    else        return 2 * pow2Rec3(n / 2) * pow2Rec3(n / 2);}

Lo mismo que lo anterior, basándonos en un árbol de estados calculamos el elemento n / 2 y lo multiplicamos por el mismo si es par el nivel de árbol si es impar como 2 * n/2 * n/2.

Quinta forma: mediante una función recursiva que básicamente es igual que que la cuarta forma pero con una variable global que vamos modificando y reducimos el número de llamadas recursivas de 4 a 1.

double cache = 0;public double pow2Rec4(int n) {    if (n == 0)        return 1;    cache = pow2Rec4(n / 2);    if (n % 2 == 0)        return cache * cache;    else        return 2 * cache * cache;}

Como vemos tenemos varias funciones, ¿pero cual es mejor? Podemos comprobarlo midiendo los tiempos.

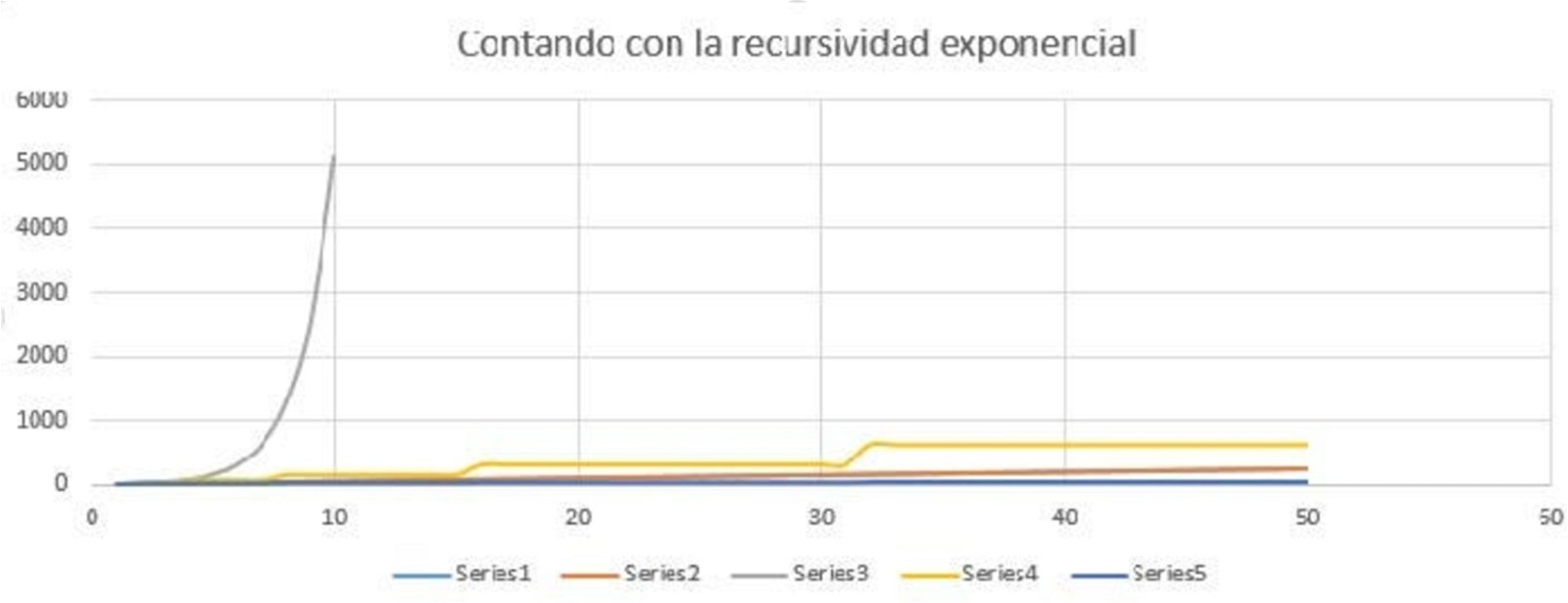
En esta primera gráfica podemos comprobar como el tiempo que tardaría la función pow2Rec2 es enorme comparado con el de las demás.

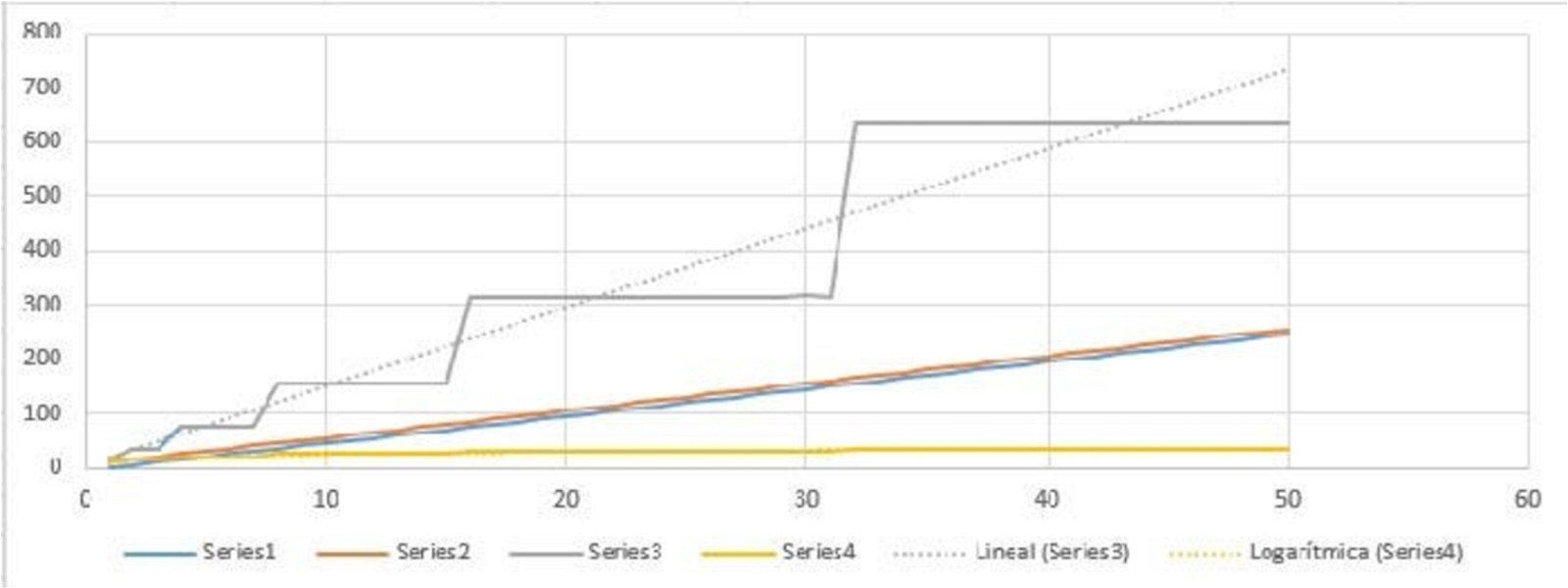
En la segunda gráfica podemos ver como todas las series (menos la powRec4) con lineales, con mayor o menor pendiente pero todas se ajustan a una recta.

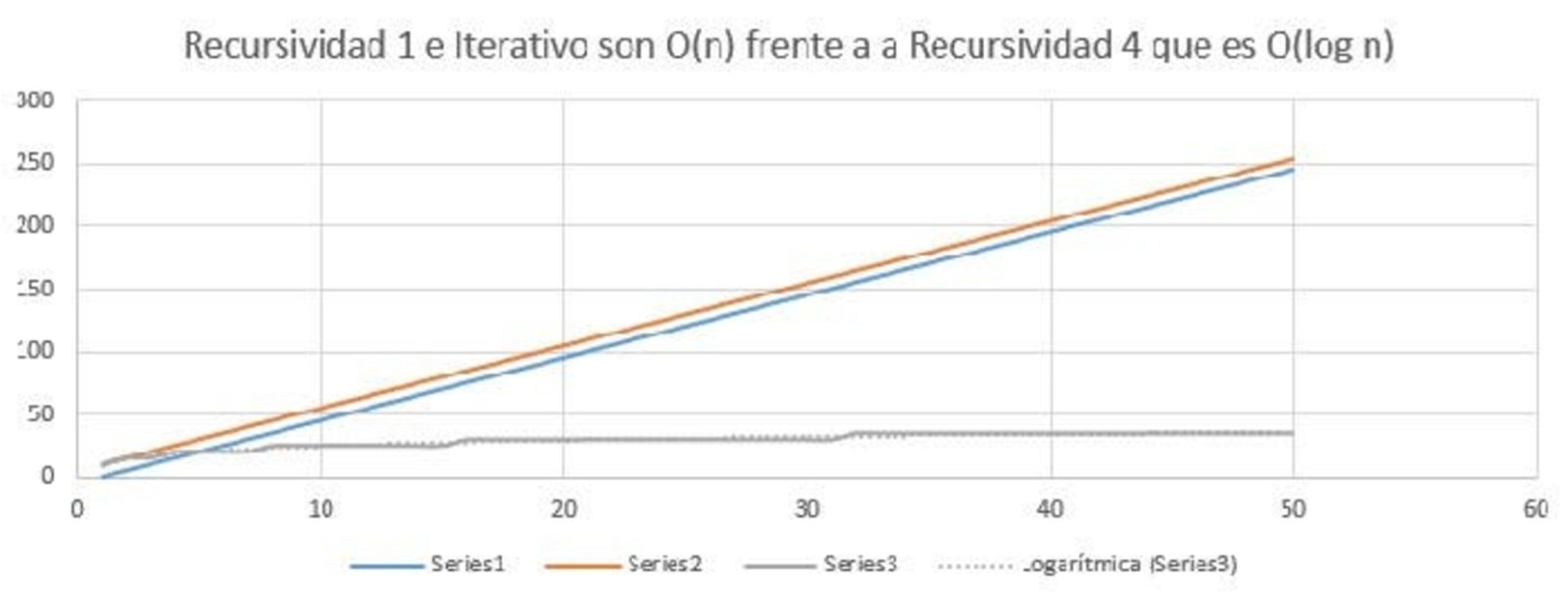
En la tercera gráfica podemos ver como el tiempo de la powRec4 crecerá de forma logarítmica y las otras se ajustarán a una recta de casi la misma pendiente.

Consecuencias de la recursividad

Básicamente la recursividad permite diseñar algoritmos que de forma iterativa generarían más código y serían menos legibles. Esto no quiere decir que el uso de la recursividad sea más apropiado que usar las funciones iterativas, no es eso. Cada técnica se debe usar en el momento idóneo, a nadie se le ocurre ir recorriendo una lista de forma recursiva de la misma forma que a nadie se le ocurre diseñar unos árboles (ya veremos lo que son) de forma iterativa. Poco a poco iremos empleando la recursividad para resolver distintos algoritmos, como por ejemplo los basados en divide y vencerás.

Podéis probar el código descargándolo de aquí.